Schwing doch mit – Resonanz

Resonanz – damit haben wir uns neulich im Physikunterricht der 12. Klasse beschäftigt. Resonanz bezieht sich hier auf Schwingungen: dass sich eine Schwingung hochschaukelt, wenn von außen etwas mit gleicher Geschwindigkeit schwingt. Das passiert zum Beispiel, wenn man ein Glas durch einen präzisen Ton zum Zerspringen bringt. Das Glas hat eine gewisse Eigenfrequenz, die man hört, wenn man gegenschnipst. Der Ton, der dabei entsteht, kommt vom Glas, welches leicht hin- und herschwingt und damit Schallwellen in die Luft setzt. Spielt man einen Ton mit genau dieser Tonhöhe, regt die schwingende Luft das Glas an, noch stärker und stärker zu schwingen: Resonanz. Solange, bis das Glas zu weit schwingt und zerbricht: die Resonanzkatastrophe.
In unserem Versuch haben wir einen elektromagnetischen Schwingkreis anstelle vom Glas benutzt. Angeregt wird der Schwingkreis durch einen Funktionsgenerator, welcher mit einstellbarer Geschwindigkeit und Stärke eine elektrische Schwingung ausgibt.
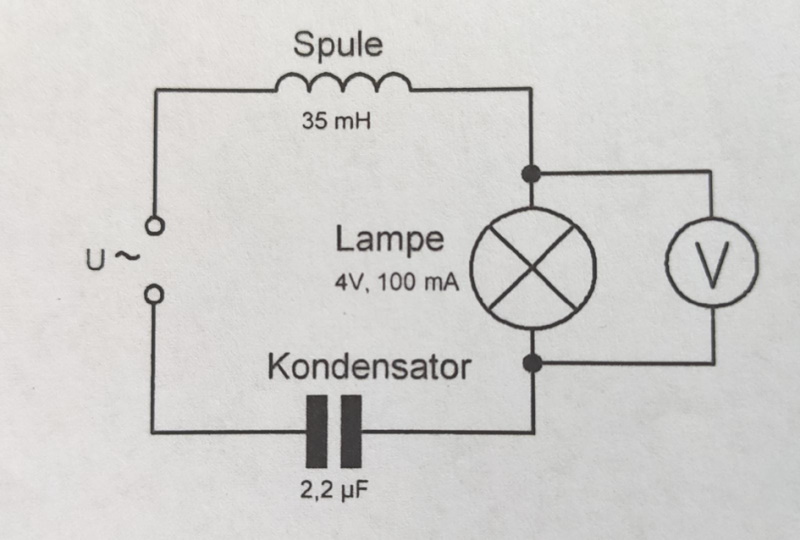
Der Kondensator und die Spule schwingen zusammen. Der Funktionsgenerator (U~) speist die Schwingung ein. An der Lampe oder am Voltmeter (V) messen wir, wie stark sich die Schwingung hochschaukelt, also die Stärke der Resonanz. Das machen wir für viele verschiedene Frequenzen, vgl. nebenstehende Tabelle.
Als Punkte in einem Koordinatensystem gezeichnet sieht das so aus:
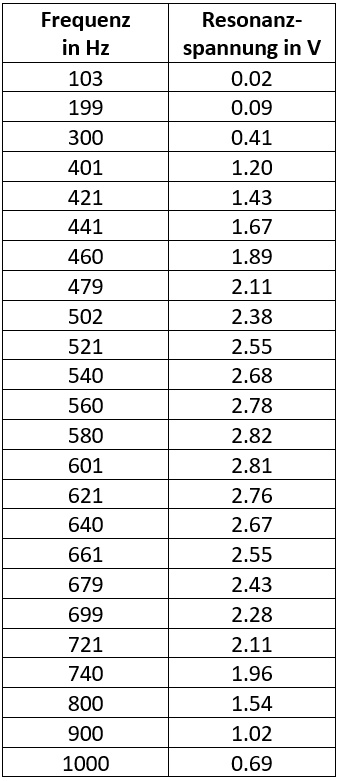
Hier kann man klar erkennen, wo die Resonanzfrequenz des elektromagnetischen Schwingkreises liegt: an der Spitze, also bei etwa 580 Hz und 2,82 V. Kann man das auch mathematisch bestätigen? Klar! Die Frequenz einer Schwingung im elektromagnetischen Schwingkreis lässt sich berechnen:
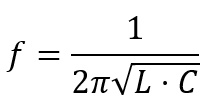
L ist die Induktivität der Spule; hier 35 mH (siehe Versuchsaufbau). C ist die Kapazität des Kondensators; hier 2,2 µF (siehe Versuchsaufbau). Damit ergibt sich:
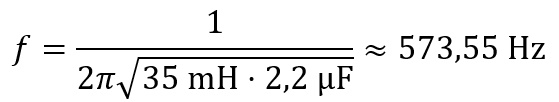
Das ist sehr nah an unseren gemessenen 580 Hz: Erfolg!